For those who have been following me on twitter, you might have noticed I’ve been playing a lot with home automation lately. I’m planning on blogging about my experiences, and how some of the pieces are put together. At this point it’s far from a full solution – just a lot of pieces and custom ugly code wired together to get some things going. In the long term, I hope to have a fully configurable and extensible home automation system, but that would probably take me a few years to get there. This is the first in a series of blogs about my experiences, and why I’m doing it the way I am. I would love to hear your inputs and ideas in the comments.
In this first post I’m going to talk about what hardware my system consists off.
Devices, protocols etc.
There’s a lot of “internet of things” devices out there already today. Unfortunately there’s also a lot of standards. And a lot of competition to get the standards to succeed. It’s like the VHS vs Betamax wars right now. Any or all might win. And some systems supports multiple. Of some of the main ones on the market today:
- Insteon / X10
- Z-Wave
- Zigbee
These standards allow devices to talk together using a common protocol, but they usually need a hub or bridge to configure it all. Several companies have then built controller hubs or bridges on top of these standards. This is where I think the entire system starts breaking down: Each company doesn’t want to help the other company, and that means each company has their own standards for talking to the controller, their website or no API at all. Another thing I’ve noticed: Most of these systems only work if you’re connected to the internet (if so the controller is usually called a “gateway”). If your internet is down you suddenly can’t control your house, your sprinklers might not run, AC is inoperable etc. And you also put a lot of trust in to that company’s security. The Heartbleed drama is a good example of why I find this really concerning. Especially considering that from their website you can see if anyone is home, disable the alarm and cameras and unlock the door, then put it all back in place as if nothing happened when they are done robbing your house. Add to that, that many controllers only works connected if you also purchase a subscription.
Lastly because all the controllers that do offer APIs, are all different. That means if I were to build a Home Automation App, I would have to either choose one of the controllers and have vendor-lock-in, meaning I would severely reduce the number of people who could use my app. Or I would have to buy all the controllers out there and build an abstraction layer. Neither of this I found very appealing either – especially considering the winning standards is still unknown.
So instead I started something else: I created my own controller software, and started to put some abstraction in into it, and uses MEF to allow extending it with more controllers – allowing others to contribute with plugins. The controller service software runs on my home PC, and is running completely offline. It’s really an “Intranet of Things”. When my phone is on the home wifi, it can talk directly to the server, and register for push updates, and the server software can push notifications to my phone, even when I’m not on the wifi. This allows me to do one-way monitoring of my phone. And if I need direct access, I can always VPN home. Lastly by not relying on a server online, I don’t have to pay, manage, scale, deal-with, build, setup etc any cloud services. It’s all self-contained – however it doesn’t prevent me from pushing data out on the internet, or connecting to a cloud service if I really wanted to.
I recently got a Galileo device, and ultimately I want to make this service run on this: 
This is just a command-line version of Windows running on a really cheap piece of hardware. That means anyone could use my server software very cheap, or just install it on a PC. Well… that’s the long term plan anyway. The WindowsOnDevices version is still in its early stages and doesn’t have everything I need yet. So for now, it runs on my PC.
The hardware I’m using
I settled on the Zigbee standard for myself (for now). I like some of the promises of Zigbee as well as some of the supported devices out there. Some of the reasons I went with Zigbee:
- Zigbee is an extremely low-power mesh network. The mesh network means the more devices you have, the better/stronger network you have. Some devices can run 10 years on a tiny battery.
- A lot of utility companies have chosen this standard to allow you to read your power consumption real-time as well as current KwH cost, total consumption etc.
- More and more companies seems to be adding support for it, meaning device prices are slowly coming down.
- Philips Hue lights uses Zigbee (these lights are cool!).
- The Nest Thermostat has a zigbee radio - not yet(?) enabled though. I’m keeping my fingers crossed…
- A friend of mine gave me a Zigbee USB controller

- The USB controller I got works directly with the Zigbee network giving me full very fine-grained control (but see cons further down)
There are some cons with Zigbee too though.
- License cost for Zigbee means the devices can be a little pricy.
- There’s several sub-standards. Zigbee HA is for home automation. Zigbee SE is a more secure version used for your smart meters. You’ll need two separate controllers to monitor both (at least they are very similar to talk to though).
- The standard is very flexible, which means it’s also pretty complex. Some controllers abstracts this away though (not mine).
- In addition there’s a new “light link” standard for HA that the Philips Hue lights run on – I believe this allow it to run controller-less. Unfortunately my HA controller doesn’t support Light Link, and the manufacturer still hasn’t updated the firmware (which btw I can’t even update myself).
- The USB Controller (or ‘coordinator’ in ZigBee speak) I have is using a VERY low-level API. It’s a lot of bit-wise operators and working with raw binary data coming in and out. It was a LOT of work just getting it working somewhat. And if you choose a different controller, most or none of my zigbee code is re-useable.
Here’s a picture of a door/window sensor, the USB coordinator and a temperature/humidity sensor.

The door sensor only uses power when it opens or closes – it’s estimated battery life is 10 years. The Temp/Humidity sensor reports measurements every 3 mins (configurable), and should last about 3 years. I have a a couple of these, plus more door sensors on the way, as well as a Philips Hue light bulb.
At this point, I wrote a little piece of software of my PC that monitors messages coming in on the ZigBee network, and turns them into push notifications. It creates a nice live-tile graph of temperature , humidity (inside and out) and recent power consumption (I’ll blog about this in a later article).
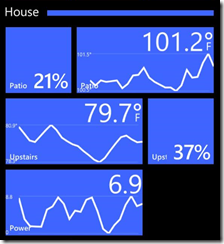
It even allows me to configure alerts when a value exceeds a certain level:
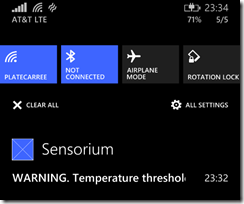
This is actually very useful when I brew beer. Since I don’t have a temperature-controlled brew-keg, this is the second best. I put the sensor in with the keg, and I get alerts on my phone when the wort is too hot or cold.

I addition I can also monitor my power consumption using a separate (but similar) Zigbee SE receiver. It sends the same graph to my phone, but my local app monitors changes in usage down to the second (I push the usage graph a lot rarer to save phone battery). It’s interesting to see what uses power and not, and how much drain it causes. You can actually see a light turn on, or when the fridge thermostat turns on and off. It’s very educational about your power consumption, and how much standby power you use. You can also read what the current cost of electricity is to help you make certain decisions.
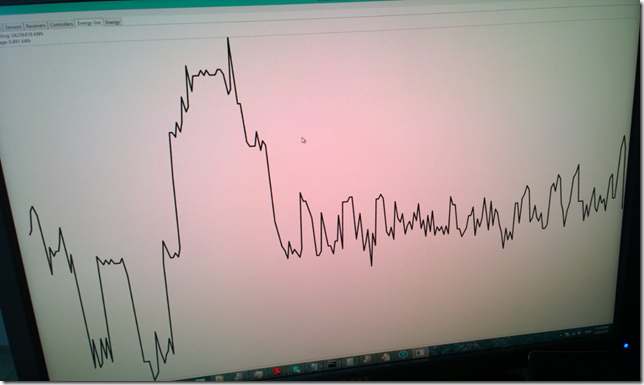
I also recorded a video of this here: 1liLQbq. You can see the graph jump 1-2 seconds after I turn a light on or off.
Some of the code for working with the Zigbee USB receiver I’ve put on Github – it’s still in a slightly rough state though: https://github.com/dotMorten/ZigbeeNet
More devices…
California is in a severe drought right now. That means there’s a lot of water restrictions in effect, including what days you can water, and what types of watering you’re allowed to do. The sprinkler time I had couldn’t automatically do this, so I just bought a new one. OpenSprinkler which is an open-source Arduino based controller. It can connect to the local network and be remotely controlled. It even has a little REST API (albeit fairly undocumented but source code is available for reverse engineering).

While the software and web interface is pretty simple, it actually works very well. It even has a Windows Phone and Windows store app (based on Cordova). I’ve also started a little project to build a .NET API for this controller so I can integrate it into my “system”. Source-code for that is all available on Github: https://github.com/dotMorten/OpenSprinklerNet
I also have a couple of ZigBee-supported AC thermostats on the way, as well as some better and prettier window sensors that I would actually considering putting up (it’s beyond me why anyone would make such an ugly sensor to mount on all windows).
What’s next
I want to build an “If this then that” style configuration for my server software. Currently all I can do is push measurements out. Next is to set up rules and make things happen with the rules are satisfied. For example “If air condition is running and a window is open, send alert”. Or “If phone/me leaves the house and a window is open, alert” Or “if it was hot, windy and dry yesterday, increase lawn watering”. Or “If outside temperature and humidity is at a certain level and inside humidity doesn’t exceed a certain level, switch from air condition to swamp cooler”. The last example is actually what got me started: I have two air condition units (upstairs and downstairs), 5 whole-house fans, and two swamp-coolers. What’s more efficient to run (or combination thereof), is quite tricky and also depends on outside and inside conditions. I live in a very old house with really poor insulation, so choosing the cheapest cooling system during the very hot summers here could save me a lot of money. A fancy rule-based system for making those decisions is what I really need. Add to that, I could tweak that decision making using weather forecasts, my current location (or my phone’s that is), and the current electricity cost.
And I want to make it pluggable. It shouldn’t just be Zigbee, or just the devices I have. I want to make it so that you can quickly add more devices and protocols by adding a plugin. It’s definitely quite a software engineering task – if you have some experience with this, I’d love to hear your design ideas. I’ll put it all on Github for people to use – and hopefully to contribute.
Then next, would be getting it all to run on the Galileo board, but there’s still some .NET and USB support lacking so for now it’ll run on a PC.
It’s a big task – it’ll take some work and time. So in the mean time I’ll be blogging about how some of the pieces are built. Stay tuned…