My recent new love when doing Silverlight Development is Expression Blend’s Interactivity API that gives you some really neat support for attaching behaviors, triggers and actions to your elements, which in turn lets you structure your code better and allows you to reuse it more often (It boggles my mind why these are not part of core Silverlight).
You can download the Expression Blend SDK for free here, but you also get it with Expression Blend 3.0.
How often haven’t you done something like this:
<Button OnClick=”ShowToolsWindow” Content=”Show Tools” />
and in the code behind:
private void ShowToolsWindow(object sender, RoutedEventArgs e)
{
ToolsWindow.Visibility = Visibility.Visible;
}While this probably isn’t much code, imagine a whole toolbar or menu each with code in two places, and especially the code-behind more or less the exact same, but with a different target. And if I remove a button, I also have to remember to remove the eventhandler. Enter triggers and actions…
With the Expression SDK we can create a trigger that does this for us.
public class ToggleVisibilityAction : TargetedTriggerAction<UIElement>
{
protected override void Invoke(object parameter)
{
this.Target.Visibility =
this.Target.Visibility == Visibility.Visible ?
Visibility.Collapsed : Visibility.Visible;
}
}What this allows us to do is the following in xaml and without using any code-behind:
<Button Content="Show Tools" Margin="20" >
<i:Interaction.Triggers>
<i:EventTrigger EventName="Click" >
<behaviors:ToggleVisibilityAction TargetName="ToolsWindow" />
</i:EventTrigger>
</i:Interaction.Triggers>
</Button>
While this might be a little more XAML than before, it cleanly separates the button into one little local piece, and also allows me to reuse the same behavior for multiple tools.
In the above case, I’m using a TargetedTriggerAction, meaning that it is triggered by one control, but acts on another. There are also non-targeted actions. For instance this one for toggling full screen:
public class ToggleFullScreenAction : TriggerAction<UIElement>
{
protected override void Invoke(object parameter)
{
Application.Current.Host.Content.IsFullScreen =
!Application.Current.Host.Content.IsFullScreen;
}
}<Button Content="Toggle Fullscreen" >
<i:Interaction.Triggers>
<i:EventTrigger EventName="Click" >
<behaviors:ToggleFullScreenAction />
</i:EventTrigger>
</i:Interaction.Triggers>
</Button>
Another more powerful item, is the behaviors. Behaviors allows us to add any logic to the control (or the application) it is attached to, when it gets attached. Basically there are two methods to override when creating a behavior: OnAttached and OnDetached. Usually this is where you will want to attach and detach eventhandlers to the element.
Here is one example that will hide an element if the application gets installed:
public class HideOnInstall : Behavior<UIElement>
{
protected override void OnAttached()
{
base.OnAttached();
Application.Current.InstallStateChanged += Current_InstallStateChanged;
}
protected override void OnDetaching()
{
base.OnDetaching();
Application.Current.InstallStateChanged -= Current_InstallStateChanged;
}
private void Current_InstallStateChanged(object sender, EventArgs e)
{
this.AssociatedObject.Visibility = (Application.Current.InstallState == InstallState.Installed)
? Visibility.Collapsed : Visibility.Visible;
}
}Now we can use that on our install button, so when the app has been installed, the button will automatically hide itself:
<Button Content="Install">
<i:Interaction.Triggers>
<i:EventTrigger EventName="Click" >
<behaviors:InstallAction />
</i:EventTrigger>
</i:Interaction.Triggers>
<i:Interaction.Behaviors>
<behaviors:HideOnInstall />
</i:Interaction.Behaviors>
</Button>
A thing that has always bothered me is that the ScrollViewer control by default doesn’t listen to MouseWheel events. Delay recently blogged about adding smooth scrolling to the scroll viewer. Based on that, I changed this to be a behavior that listens to the MouseWheel event.
To do this we first create a behavior that inherits from Behavior<ScrollViewer>. This ensures that the behavior can only be attached to a ScrollViewer. In OnAttached we start listening for the MouseWheel event:
protected override void OnAttached()
{
AssociatedObject.MouseWheel += AssociatedObject_MouseWheel;
base.OnAttached();
}In the event handler we just call AssociatedObject.ScrollToVerticalOffset(offset) to apply the scroll (The sample you can download here goes a little further and uses a DoubleAnimation with easing to make the scrolling more smooth). Now to add MouseWheel scrolling support to all scroll viewers, all you need to do is add the behavior to the scroll viewer:
<ScrollViewer>
<i:Interaction.Behaviors>
<behaviors:MouseScrollViewer />
</i:Interaction.Behaviors>
</ScrollViewer>
The neat thing about these behaviors is that you get drag’n’drop behavior inside Expression Blend. This means that you can simply drag these from the Assets window right on to your elements without having to touch any code or XAML. Here’s what my sample application looks like in the objects and assets windows:
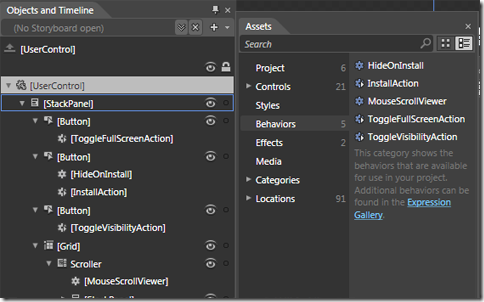
When I migrated this application from Silverlight 2 to 3, I managed to remove almost 70% of the code-behind in page.xaml.cs mostly caused by reusing simple actions and behaviors, and separating the logic into reusable classes instead. Later I found myself often going back to grab these classes and re-use them for other projects.
You can try out the sample application here and download the code here.